某企业投资所要求的最低报酬率为8%,现有三个方案,有关数据如表。计算投资风险。
正确答案:
1.风险程度计算
先来考察A方案,各年现金流入的风险程度可用期望现金流入的方差来衡量,三年现金流入的总的离散程度,即综合标准差:
为了比较不同规模项目的风险大小,引入变化系数的概念:变化系数是标准差与期望值的
比值,是用相对数表示的离散程度即风险的大小。为了综合各年的风险,对具有一系列现金流入的方案用综合变化系数来反映,即:
Q=综合标准差/现金流入预期现值=D/EPV则
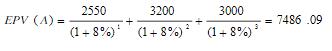
Q(A)=1942/2486=0.2594 2.确定风险报酬斜率
风险报酬斜率是方程K=i+bQ的系数b,b的取值来源于经验数据,可依据历史资料或直线回归法测出。
一般认为,中等风险程度的项目变化系数为0.5,假定含有风险报酬的最低报酬率为12%,无风险报酬率为8%时,则有:
b=(12%-8%)/0.5=0.08
由于A方案的综合变化系数Q(A)=0.259,所以A方案的风险调整贴现率K(A)=8%+0.08×0.259=10%
同理可得B、C方案的风险调整贴现率分别为K(B)=9.26%,K(C)=8.84% 根据不同的风险调整贴现率计算的净现值:
NPV(A)=2550/(1+10%)1+3200/(1+10%)2+3000/(1+10%)3-6000=1217(元)NPV(B)=4000/(1.0926)2-3000=350(元);NPV(C)=3800/(1.0884)3-3000=-52.66(元)
由此,以上三个方案的优劣顺序为A>B>C。
先来考察A方案,各年现金流入的风险程度可用期望现金流入的方差来衡量,三年现金流入的总的离散程度,即综合标准差:

为了比较不同规模项目的风险大小,引入变化系数的概念:变化系数是标准差与期望值的
比值,是用相对数表示的离散程度即风险的大小。为了综合各年的风险,对具有一系列现金流入的方案用综合变化系数来反映,即:
Q=综合标准差/现金流入预期现值=D/EPV则
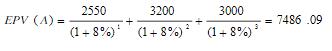
Q(A)=1942/2486=0.2594 2.确定风险报酬斜率
风险报酬斜率是方程K=i+bQ的系数b,b的取值来源于经验数据,可依据历史资料或直线回归法测出。
一般认为,中等风险程度的项目变化系数为0.5,假定含有风险报酬的最低报酬率为12%,无风险报酬率为8%时,则有:
b=(12%-8%)/0.5=0.08
由于A方案的综合变化系数Q(A)=0.259,所以A方案的风险调整贴现率K(A)=8%+0.08×0.259=10%
同理可得B、C方案的风险调整贴现率分别为K(B)=9.26%,K(C)=8.84% 根据不同的风险调整贴现率计算的净现值:
NPV(A)=2550/(1+10%)1+3200/(1+10%)2+3000/(1+10%)3-6000=1217(元)NPV(B)=4000/(1.0926)2-3000=350(元);NPV(C)=3800/(1.0884)3-3000=-52.66(元)
由此,以上三个方案的优劣顺序为A>B>C。
答案解析:有

微信扫一扫手机做题
