如图所示,质量为M,长为的均匀直棒,可绕垂直于棒一端的水平轴O无摩擦地转动,它原来静止在平衡位置上,现有一质量为的弹性小球飞来,正好在棒的下端与棒垂直地相撞,相撞后,使棒从平衡位置处摆动到最大角度θ=30°处, (1)设这碰撞为弹性碰撞,试计算小球初速v0的值; (2)相撞时小球受到多大的冲量? 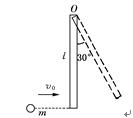
正确答案:
(1)设小球的初速度为v0,棒经小球碰撞后得到的初角速度为ω,而小球的速度变为v,按题意,小球和棒作弹性碰撞,所以碰撞时遵从角动量守恒定律和机械能守恒定律,可列式:
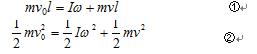
上两式中I=(1/3)Ml2,碰撞过程极为短暂,可认为棒没有显著的角位移;碰撞后,棒从竖直位置上摆到最大角度θ=30°,按机械能守恒定律可列式:

(2)相碰时小球受到的冲量为
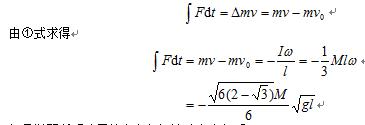
负号说明所受冲量的方向与初速度方向相反。
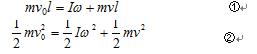
上两式中I=(1/3)Ml2,碰撞过程极为短暂,可认为棒没有显著的角位移;碰撞后,棒从竖直位置上摆到最大角度θ=30°,按机械能守恒定律可列式:

(2)相碰时小球受到的冲量为
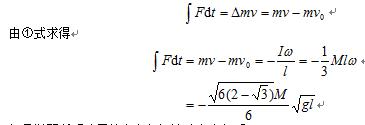
负号说明所受冲量的方向与初速度方向相反。
答案解析:有

微信扫一扫手机做题
