假设货币需求L=0.2Y-5r,货币供给M=200,消费C=60+0.8Yd ,税收T=100,投资I=150-5r,政府支出G=100。求: (1)IS 和LM 方程及均衡收入、利率和投资; (2)若其他情况不变,政府支出从100增加到120时,均衡收入、利率和投资变为多少? (3)是否存在“挤出效应”?为什么?
正确答案:(1)由Y=C+I+G
=60+0.8 Yd +150-5r+100
=310+0.8×(Y-100)-5r
化简得:0.2Y=230-5r Y=1150-25r (IS 曲线)
由L=0.2Y-5r,M=200 和L=M 得 0.2Y-5r=200 Y=1000+25r (LM 曲线)
由IS-LM模型联立方程组:
解得:Y=1075 ,r=3, I=135
即均衡收入、均衡利率和投资分别为1025、3%和135。
(2)由C=60+0.8 Y d,T=100,I=150-5r, G=120 和Y=C+I+G得IS曲线为:
Y=C+I+G
=60+0.8 Y d,+150-5r+120
=330+0.8(Y-100)-5r
=250+0.8Y-5r
化简得:Y=1250-25r (IS 曲线)
由L=0.2Y-5r, M=200 和L=M得LM曲线为:
0.2Y-5r=200 Y=1000+25r (LM 曲线)
由IS—LM 模型联立: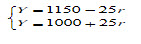
解得:均衡收入为Y=1125,均衡利率r=5, 投资I=125
(3)因为政府支出增加,使得私人投资135减少为125,所以存在“挤出效应”。政府支出增加“挤占”了私人投资。
=60+0.8 Yd +150-5r+100
=310+0.8×(Y-100)-5r
化简得:0.2Y=230-5r Y=1150-25r (IS 曲线)
由L=0.2Y-5r,M=200 和L=M 得 0.2Y-5r=200 Y=1000+25r (LM 曲线)
由IS-LM模型联立方程组:

解得:Y=1075 ,r=3, I=135
即均衡收入、均衡利率和投资分别为1025、3%和135。
(2)由C=60+0.8 Y d,T=100,I=150-5r, G=120 和Y=C+I+G得IS曲线为:
Y=C+I+G
=60+0.8 Y d,+150-5r+120
=330+0.8(Y-100)-5r
=250+0.8Y-5r
化简得:Y=1250-25r (IS 曲线)
由L=0.2Y-5r, M=200 和L=M得LM曲线为:
0.2Y-5r=200 Y=1000+25r (LM 曲线)
由IS—LM 模型联立:
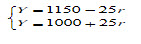
解得:均衡收入为Y=1125,均衡利率r=5, 投资I=125
(3)因为政府支出增加,使得私人投资135减少为125,所以存在“挤出效应”。政府支出增加“挤占”了私人投资。
答案解析:有

微信扫一扫手机做题
