求证: ①倒格矢Gh=h1b1+h2b2+h3b3垂直于米勒指数为(h1h2h3)的晶面系。(斜体代表矢量) ②如果正格子(h1h2h3)晶面系的面间距为d,则倒格子Gh=h1b1+h2b2+h3b3的长度为2π/d。
正确答案:
①取原点最近的一个面在晶胞基矢上所截的矢量OH,OK,OL分别为a1/h1,a2/h2,a3/h3,
则:HK=a2/h2-a1/h1,KL=a3/h3-a2/h2,LH=a1/h1-a3/h3,
其中HK、KL、LH所在直线为互不平行的共面直线。又
因为Gh〃HK=Gh〃KL=Gh〃LH=0,所
所以Gh分别垂直于这三条直线,
因此Gh垂直于米勒指数为(h1h2h3)的晶面系。
如图:

②Gh垂直于(h1h2h3),设其相交于点M,则OM=d,而OM又是正格子基矢a1在Gh上的投影。
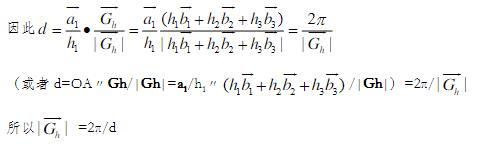
如图:

则:HK=a2/h2-a1/h1,KL=a3/h3-a2/h2,LH=a1/h1-a3/h3,
其中HK、KL、LH所在直线为互不平行的共面直线。又
因为Gh〃HK=Gh〃KL=Gh〃LH=0,所
所以Gh分别垂直于这三条直线,
因此Gh垂直于米勒指数为(h1h2h3)的晶面系。
如图:

②Gh垂直于(h1h2h3),设其相交于点M,则OM=d,而OM又是正格子基矢a1在Gh上的投影。
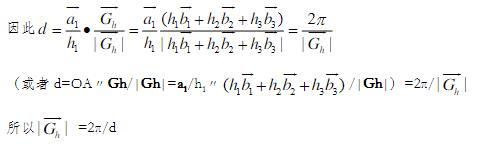
如图:

答案解析:有

微信扫一扫手机做题
