同轴电缆由导体圆柱和一同轴导体薄圆筒构成,电流I从一导体流入,从另一导体流出,且导体上电流均匀分布在其横截面积上,设圆柱半径为R1,圆筒半径为R2,如图所示.求: (1)磁感应强度B的分布; (2)在圆柱和圆筒之间单位长度截面的磁通量为多少? 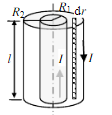
正确答案:(1)导体圆柱的面积为S=πR12,面电流密度为δ=I/S=I/πR12。
在圆柱以半径r作一圆形环路,其面积为Sr=πr2包围的电流是Ir=δSr=Ir2/R12.
由于B与环路方向相同,积分得2πrB=μ0Ir,
所以磁感应强度为B=μ0Ir/2πR12,在两导体之间作一半径为r的圆形环中,
所包围的电流为I,根据安培环中定理可得B=μ0I/2πr,R1在圆筒之外作一半径为r的圆形环中,由于圆柱和圆筒通过的电流相反,所包围的电流为零,根据安培环中定理可得B=0,(r>R2).
(2)在圆柱和圆筒之间离轴线r处作一径向的长为l=1、宽为dr的矩形,其面积为dS=ldr=dr,方向与磁力线的方向一致,通过矩形的磁通量为dΦ=BdS=Bdr,
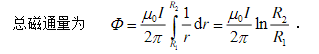
在圆柱以半径r作一圆形环路,其面积为Sr=πr2包围的电流是Ir=δSr=Ir2/R12.
由于B与环路方向相同,积分得2πrB=μ0Ir,
所以磁感应强度为B=μ0Ir/2πR12,
所包围的电流为I,根据安培环中定理可得B=μ0I/2πr,R1
(2)在圆柱和圆筒之间离轴线r处作一径向的长为l=1、宽为dr的矩形,其面积为dS=ldr=dr,方向与磁力线的方向一致,通过矩形的磁通量为dΦ=BdS=Bdr,
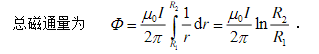
答案解析:有

微信扫一扫手机做题


