用表上作业法求给出运输问题的最优解（M是任意大正数）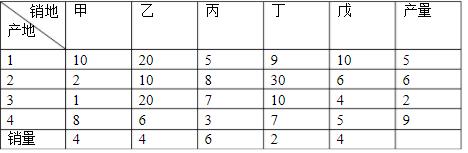

正确答案:此问题是一个产销不平衡的问题，产大于销。增加一个假象销售地己，令单位运价为0。销量为2。这样就达到了产销平衡。
用伏格尔法求初始解：
①计算出各行和各列的次最小运费和最小运费的差额，填入该表的最右列和最下列。
②从行差额或者列差额中找出最大的，选择它所在的行或者列中的最小元素，产地1所在的行是最大差额行，最小元素0，说以一产地的产品应该优先供应己的需要，同时划掉己列的数字。
③对上表中的元素分别计算各行和各列的次最小运费和最小运费的差额，填入该标的最右列和最下行，重复步骤①②，直到求出初始解为止。得到下表：

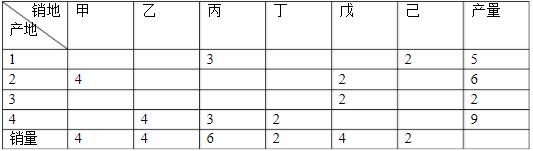
使用位势法进行检验：
①上表中，数字格处填入单位运价，并增加一行一列，在列中填入u_i（i=1，2，3，4），在行中填入v_j（j=1，2，3，4，5，6），先令u₁=0，由u_i+v_i=c_ij（i，j∈B，B为基，下同）来确定u_i和v_i
②由σ_ij=c_ij-（u_i+v_i）（i，j∈N）计算所有空格的检验数，在每个格的右上角填入单位运价。
由上表可以看出，所有的非基变量检验数≥0，此问题达到最优解。
又因为σ₁₄=0，此问题有无穷多最优解。
总运费min z=90