什么是单位脉冲函数δ(t)?它有什么特性?如何求其频谱?
正确答案:
在ε时间内矩形脉冲δε(t)(或三角形脉冲及其他形状脉冲)的面积为1,当ε→0时,δε(t)的极限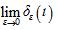 ,称为δ函数。δ函数用标有“1”的箭头表示。显然δ(t)的函数值和面积(通常表示能量或强度)分别为:
,称为δ函数。δ函数用标有“1”的箭头表示。显然δ(t)的函数值和面积(通常表示能量或强度)分别为:
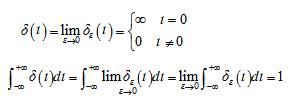
⑵δ(t)函数的性质
①积分筛选特性。
当单位脉冲函数δ(t)与一个在t=0处连续且有界的信号x(t)相乘时,其积的积分只有在t=0处得到x(0),其余各点乘积及积分均为零,从而有:
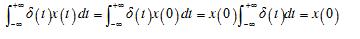
这就表明,当连续时间函数x(t)与单位冲激信号δ(t)或者δ(t-t0)相乘,并在(-∞,+∞)时间内积分,可得到x(t)在t=0点的函数值x(0)或者t=t0点的函数值x(t0),即筛选出x(0)或者x(t0)。
②冲击函数是偶函数,即δ(t)=δ(-t)。
③乘积(抽样)特性:
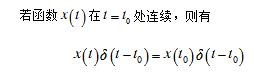
④卷积特性:
任何连续信号x(t)与δ(t)的卷积是一种最简单的卷积积分,结果仍然是该连续信号x(t),即
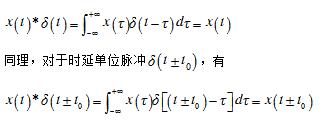
可见,信号x(t)和δ(t±t0)函数卷积的几何意义,就是使信号x(t)延迟±t0脉冲时间。
⑶δ(t)函数的频谱
单位脉冲信号的傅立叶变换等于1,其频谱如下图所示,这一结果表明,在时域持续时间无限短,幅度为无限大的单位冲击信号,在频域却分解为无限宽度频率范围内幅度均匀的指数分量。

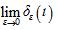 ,称为δ函数。δ函数用标有“1”的箭头表示。显然δ(t)的函数值和面积(通常表示能量或强度)分别为:
,称为δ函数。δ函数用标有“1”的箭头表示。显然δ(t)的函数值和面积(通常表示能量或强度)分别为: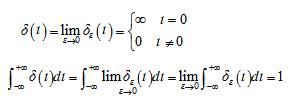
⑵δ(t)函数的性质
①积分筛选特性。
当单位脉冲函数δ(t)与一个在t=0处连续且有界的信号x(t)相乘时,其积的积分只有在t=0处得到x(0),其余各点乘积及积分均为零,从而有:
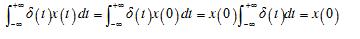
这就表明,当连续时间函数x(t)与单位冲激信号δ(t)或者δ(t-t0)相乘,并在(-∞,+∞)时间内积分,可得到x(t)在t=0点的函数值x(0)或者t=t0点的函数值x(t0),即筛选出x(0)或者x(t0)。
②冲击函数是偶函数,即δ(t)=δ(-t)。
③乘积(抽样)特性:
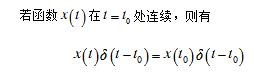
④卷积特性:
任何连续信号x(t)与δ(t)的卷积是一种最简单的卷积积分,结果仍然是该连续信号x(t),即
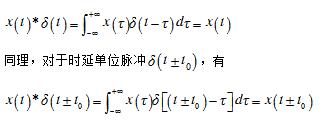
可见,信号x(t)和δ(t±t0)函数卷积的几何意义,就是使信号x(t)延迟±t0脉冲时间。
⑶δ(t)函数的频谱
单位脉冲信号的傅立叶变换等于1,其频谱如下图所示,这一结果表明,在时域持续时间无限短,幅度为无限大的单位冲击信号,在频域却分解为无限宽度频率范围内幅度均匀的指数分量。

答案解析:有

微信扫一扫手机做题
