【背景材料】已知网络计划如图3-20所示，箭线下方括号外数字为工作的正常持续时间，括号内数字为工作的最短持续时间；箭线上方括号内数字为优选系数，要求工期为12天。 试对其进行工期优化。

正确答案: （1）用标号法找出初始网络计划的计算工期和关键线路。
如图3-21所示：T_C=15天，关键线路为：1→3→5→6。

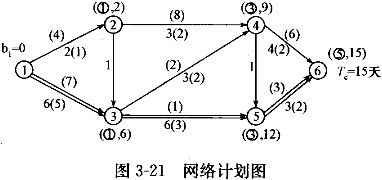
（2）因Tc=15天，Tr=12天，故应压缩的工期为△T=Tc-Tr=15-12=3天。
（3）在关键工作1-3，3-5，5-6中，3-5工作的优选系数最小，应优先压缩。
（4）将关键工作3-5的持续时间由6天压缩成3天，这时的关键线路为1→3→4→6，不经过1→3→5→6，故关键工作3-5被压缩成非关键工作，这是不合理的。
将3-5的持续时间压缩到4天，这时关键线路有三条，分别为1→3→5→6，1→3→4→5→6和1→3→4→6，如图3-22所示，这时关键工作3-5仍然为关键工作，所以是可行的。
（5）第1次压缩后，计算工期Tc=13天，仍然大于要求工期Tr，故需要继续压缩。此时，网络图中有3条关键线路，要想有效缩短工期，必须在每条关键线路上压缩相同数值。
在图3-22所示网络计划中，有以下4种方案：
①压缩工作1-3，优选系数为7；
②同时压缩工作3-4和3-5，组合优选系数为：2+1=3；
③同时压缩工作3-4和5-6，组合优选系数为：2+3=5；
④同时压缩工作4-6和5-6，组合优选系数为：6+3=9。
上述四种方案中，由于同时压缩工作3-4和3-5，组合优选系数最小，故应选择同时压缩工作3-4和3-5的方案。

（6）将工作3-4和3-5的持续时间同时压缩1天，此时重新用标号法计算网络计划时间参数，关键线路仍为3条，即：1→3→4→6和1→3→4→5→6及1→3→5→6，关键工作3-4和3-5仍然是关键工作，所以第2次压缩是可行的。
（7）经第2次压缩后，网络计划如图3-23所示，此时计算工期Tc=12天，满足要求工期Tc。故经过2次压缩达到了工期优化的目标。