某企业拥有一辆汽车，价值30万元。如果投保，保费为0.5万元。假定这种汽车毁损的情况只有两种：①l%的概率全损；②99%的概率无损失。本题不考虑不可保损失。风险管理者可能采取的风险处理方案的损失矩阵如下： （1）假设税率为50%，请建立税后损失矩阵。  （2）在Minmax原则和Minmin原则下，决策者应分别选择何种方案？ （3）如果以损失期望值最小为标准，决策者应选择哪种方案？  （4）假设损失矩阵中考虑忧虑价值为0.2万元，则决策者应选择何种方案？ （5）如果决策者选择购买保险，那么忧虑价值至少为多少？  （6）忧虑价值如果为0.2万元，而决策者选择购买保险，那么汽车全损概率应为多少

正确答案:（1）

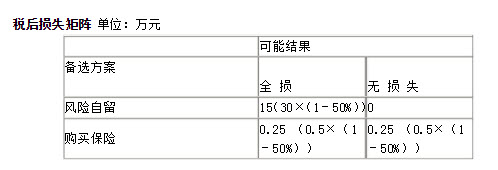
（2）在Minmax原则和Minmin原则下，应该选择购买保险方案，因为两者方案的最大潜在损失分别为30万元，0.5万元。
（3）分别计算各方案的损失期望值：
①风险自留：E1=15×1%＋0×99%=0.15（万元）
②购买保险：E2=0.25×1%＋0.25×99%=0.25（万元）
这里E2> E1，按照损失期望值原则，风险自留方案最佳，即应该选择风险自留的方案。
（4） 考虑价值之后的税后风险损失矩阵为：
根据上面的损失矩阵，可以计算各方案的损失期望值：
风险自留：E1=15.2×1%＋0.2×99%=0.35（万元）购
买保险：E2=0.25×1%＋0.25×99%=0.25（万元）E
1>E2，按照损失期望值的原则，方案2为最佳方案。 
（5） 假设忧虑价值为X，那么有：
①风险自留：E1=（15＋X）×1%＋X×99% 
②购买保险：E2=0.25×1%＋0.25×99%
如果决策者选择购买保险，那么E1> E2 ，即（15＋X）×1%＋X×99%1>0.25×1%＋0.25×99%，解得：X≥0.1万元
（6）假设汽车完全损失的概率为P，则由期望损失的原则可得： （15＋0.2）×P＋0.2×（1－P）≥0.25×P＋0.25×（1－P） 可以得到P≥ 1/300