已知一简谐振子的振动曲线如图所示，试由图求： （1）a，b，c，d，e各点的位相，及到达这些状态的时刻t各是多少？已知周期为T；  （2）振动表达式；  （3）画出旋转矢量图．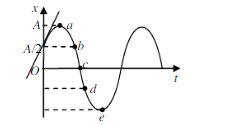

正确答案: （1）设曲线方程为x=AcosΦ，其中A表示振幅，Φ=ωt+θ表示相位.
由于xa=A，所以cosΦa=1，因此  Φa=0.
由于xb=A/2，所以cosΦb=0.5，因此 Φb=±π/3；
由于位相Φ随时间t增加，b点位相就应该大于a点的位相，因此 Φb=π/3.
由于xc=0，所以cosΦc=0，
又由于c点位相大于b位相，因此Φc=π/2.
同理可得其他两点位相为：Φd=2π/3，Φe=π.c点和a点的相位之差为π/2，时间之差为T/4，而b点和a点的相位之差为π/3，时间之差应该为T/6.因为b点的位移值与O时刻的位移值相同。
所以到达a点的时刻为ta=T/6.
到达b点的时刻为tb=2ta = T/3.
到达c点的时刻为tc=ta+T/4=5T/12.
到达d点的时刻为td=tc+T/12=T/2.
到达e点的时刻为te=ta+T/2=2T/3.
（2）设振动表达式为：x=Acos（ωt+θ），
当t=0时，x=A/2时，所以cosθ=0.5，因此θ=±π/3；由于零时刻的位相小于a点的位相，所以θ=-π/3，因此振动表达式为
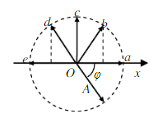
（3）