以保险市场为例,说明消费者在不确定条件下是如何进行选择的。
正确答案:
假定消费者考虑为一项价值为a的财产投火灾保险,投保需要支付的数额为Q。为了简单起见,设火灾发生,消费者的损失为b,并且只要火灾发生,保险公司就向投保人支付价值为q的补偿金。于是,消费者购买保险这一行为的结果是:若发生火灾,其财产价值为a1=a–b–Q+q;若没有发生火灾,其财产价值为a2=a –Q。若假定发生火灾的概率是α,则消费者购买保险的期望效用为: αU(a1)+(1-α)U(a2)
再定义每获得1单位补偿需要支付的费用为保险的价格,即P=Q/q,并假定它是由市场供求所决定的一个常数。这样,消费者在既定的价格下,选择适当的Q以便效用为最大。利用Q=Pq,则消费者购买保险的行为可以描述为:
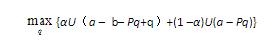
根据效用最大化的条件,上式右面关于q的一阶导数为0,所以有: αU’(a1)(1-P)-P(1-α)U’(a2)=0
其中,U’(a1)和U’(a2)分别为消费者在a1和a2处的边际效用。经过整理可以得到:
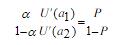
上式中,U’(a1)/U’(a2)可以理解为消费a1和a2时的边际替代率,而α和(1-α)分别是发生和不发生火灾的概率,于是,它的左边是不确定性条件下的边际替代率,而右边则是购买保险在出现火灾和未出现火灾时的价格之比。
与确定性条件下的选择一样,上式既是消费者获得效用最大化的条件,也决定了消费者对保险数量的需求(函数)。因此,不确定性条件下的选择只不过是确定性条件下的选择的一个推广。
再定义每获得1单位补偿需要支付的费用为保险的价格,即P=Q/q,并假定它是由市场供求所决定的一个常数。这样,消费者在既定的价格下,选择适当的Q以便效用为最大。利用Q=Pq,则消费者购买保险的行为可以描述为:
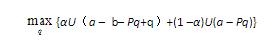
根据效用最大化的条件,上式右面关于q的一阶导数为0,所以有: αU’(a1)(1-P)-P(1-α)U’(a2)=0
其中,U’(a1)和U’(a2)分别为消费者在a1和a2处的边际效用。经过整理可以得到:
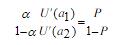
上式中,U’(a1)/U’(a2)可以理解为消费a1和a2时的边际替代率,而α和(1-α)分别是发生和不发生火灾的概率,于是,它的左边是不确定性条件下的边际替代率,而右边则是购买保险在出现火灾和未出现火灾时的价格之比。
与确定性条件下的选择一样,上式既是消费者获得效用最大化的条件,也决定了消费者对保险数量的需求(函数)。因此,不确定性条件下的选择只不过是确定性条件下的选择的一个推广。
答案解析:有

微信扫一扫手机做题
