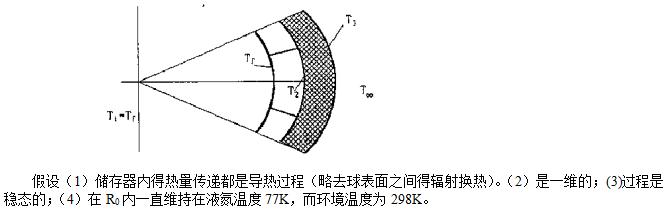
一种存放液氮的钢制球形容器如附图所示。它由两层同心钢制球壳(第一层的内、外半径分别为R0、R1,第二层的内外半径分别为R2、R3)及求外的保温层(内、外半径分别为R3、R4)组成。在第一层球壳及第二层球壳之间(R12)为真空,且半径为R1、R2的球面抛光良好而可作为理想的反射体。这两层球壳之间用对称布置的4个圆锥状实心柱体支撑(见附图,w=2.4×10-2sr),其导热系数为温度的线性函数,并已知:T=50K时λ=0.05W/(m·K),T=300K时λ=5W/(m·K);钢壳的导热系数也是温度的线性函数,且T=50K时λ=5W/(m·K),T=300K时λ=15W/(m·K)。保温材料为玻璃棉,λ=3×10-2W/(m·K),可视为常数。77K的液态氮存储于半径为R1的球容器中,其汽化潜热r=2×102kj/kg,ρ=808kg/m3。环境温度T∞=298K。R0=0.149m,R1=0.150m,R2=0.200m,R3=0.201m,R4=0.300m,保温层外表面复合换热的表面传热系数h=10W/(m2·K)。试计算该钢制球形容器中存放的50%容积的液氮经多少天可能全部蒸发掉。假定过程时稳态的。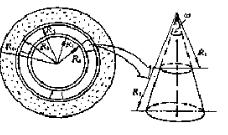
答案解析:有