股票现价为$40。已知在一个月后股价为$42或$38。无风险年利率为8%(连续复利)。执行价格为$39的1个月期欧式看涨期权的价值为多少?
正确答案:
考虑一资产组合:卖空1份看涨期权;买入Δ份股票。
若股价为$42,组合价值则为42Δ-3;若股价为$38,组合价值则为38Δ
当42Δ-3=38Δ,即Δ=0.75时,
组合价值在任何情况下均为$28.5,其现值为: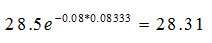
即:-f+40Δ=28.31,其中f为看涨期权价格。
所以,f=40×0.75-28.31=$1.69
另解:(计算风险中性概率p)
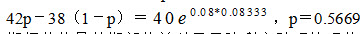
期权价值是其期望收益以无风险利率贴现的现值,即:
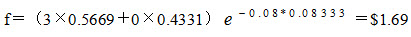
若股价为$42,组合价值则为42Δ-3;若股价为$38,组合价值则为38Δ
当42Δ-3=38Δ,即Δ=0.75时,
组合价值在任何情况下均为$28.5,其现值为:
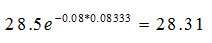
即:-f+40Δ=28.31,其中f为看涨期权价格。
所以,f=40×0.75-28.31=$1.69
另解:(计算风险中性概率p)
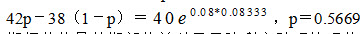
期权价值是其期望收益以无风险利率贴现的现值,即:
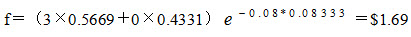
答案解析:有

微信扫一扫手机做题
