设配送中心0向7个客户Pi(i=1,…,7)配送货物。从配送中心到客户的距离为dOj(j=1,…,7)公里,各客户之间的距离为dij(i=1,…,7;j=1,…,7)公里,如表 4-5所示(表中数字单位:公里)。 请用节约法求从配送中心出发配送货物的最短路线。
正确答案:
根据节约法的思想,设节约里程为Sij(i=1,…,4;j=1,…,4),则Sij为i和j两个用户离物流中心距离的之和再减去i和j之间的距离所得的值,即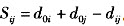 。那么
。那么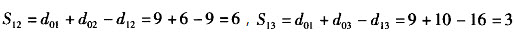 ,依此类推,可以得到各用户之间的Sij值如表4-6所示。
,依此类推,可以得到各用户之间的Sij值如表4-6所示。
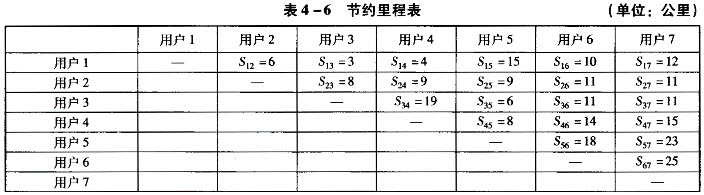 根据表4-6可得节约里程数的大小顺序如表4-7所示。
根据表4-6可得节约里程数的大小顺序如表4-7所示。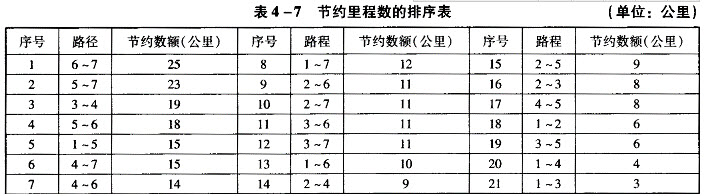
根据节约法的思想,首先选择节约里程数最大的路段,即(6~7),然后是(5~7),接下来依次为(1~5),(1~2),(2~4),(3~4);
因此,其配送路线为:0→6→7→5→1→2→4→3→0;
总路程为: ;
;
则从配送中心出发的最短配送路线为:配送中心→用户(6)→用户(7)→用户(5)→用户(1)→用户(2)→用户(4)→用户(3)→配送中心;从中心出发最短的配送里程为69公里。
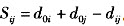 。那么
。那么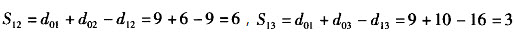 ,依此类推,可以得到各用户之间的Sij值如表4-6所示。
,依此类推,可以得到各用户之间的Sij值如表4-6所示。 根据表4-6可得节约里程数的大小顺序如表4-7所示。
根据表4-6可得节约里程数的大小顺序如表4-7所示。
根据节约法的思想,首先选择节约里程数最大的路段,即(6~7),然后是(5~7),接下来依次为(1~5),(1~2),(2~4),(3~4);
因此,其配送路线为:0→6→7→5→1→2→4→3→0;
总路程为:
 ;
;则从配送中心出发的最短配送路线为:配送中心→用户(6)→用户(7)→用户(5)→用户(1)→用户(2)→用户(4)→用户(3)→配送中心;从中心出发最短的配送里程为69公里。
答案解析:有

微信扫一扫手机做题


